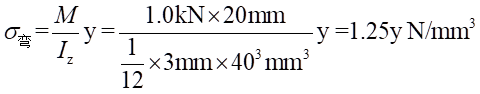偏心拉压实验
一、实验目的
1.测定如图5-2所示试件,沿
A-A加载时,即偏心拉伸时的拉应力和弯曲应力。
2.测定如图5-2所示试件,沿
A-A加载时,即偏心拉伸截面中性轴位置。
3.与理论值进行比较分析。
二、实验仪器和设备
1.拉压实验装置一台。
2.静态数字电阻应变仪一台。
3.偏心拉伸试件一根(已粘贴好应变片)。
三、实验原理及步骤
1. 实验原理
拉压实验装置见图5-1,试件(见图5-2)就被安装在上、下夹具中间进行加载。
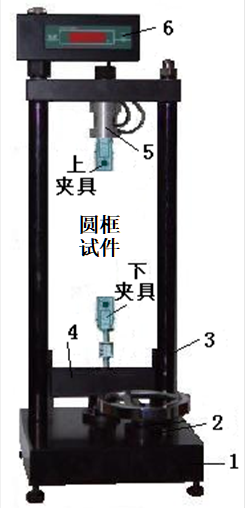
图5-1 拉压装置图
当载荷加载在试件的对称轴上,试件的横截面上只受到轴力,因此又有拉伸正应力。同样,当载荷加载到了试件的A-A截面上时,此时由拉力引起的正应力和轴对称加载时产生的拉应力是一样的,应力为:
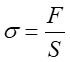
(5-1)
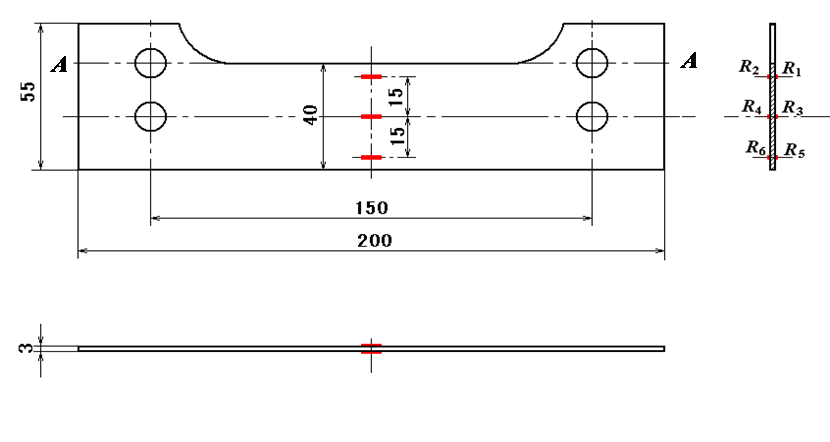
图5-2 试件贴片图
但是,当载荷加载到了试件的A-A截面时,试件横截面上由此产生的正应力分为两部分,其一是拉力
F引起的拉伸应力
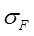
,另一部分是弯曲引起的正应力
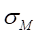
。因此当载荷加载在A-A截面上时,试件横截面上的正应力为:
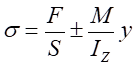
(5-2)
其中,
F表示轴力,
S表示横截面面积,
M=0.22
F表示横截面上的弯矩,
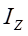
为形心轴惯性矩,
y为距离中性轴的距离(见图5-3)
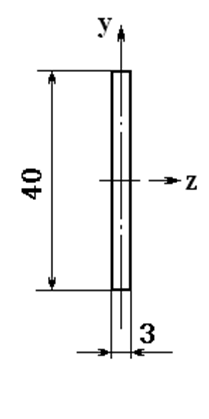
图5-3 试件横截面图
偏心拉伸试件材料弹性模量为70GN/m
2。
试件上的贴片情况(见图5-4),其中对应正反面的应变片已两两串联连接。另有一补偿块,补偿块上共粘贴了四片应变片,其中绿色线为两片应变片串联连接线。
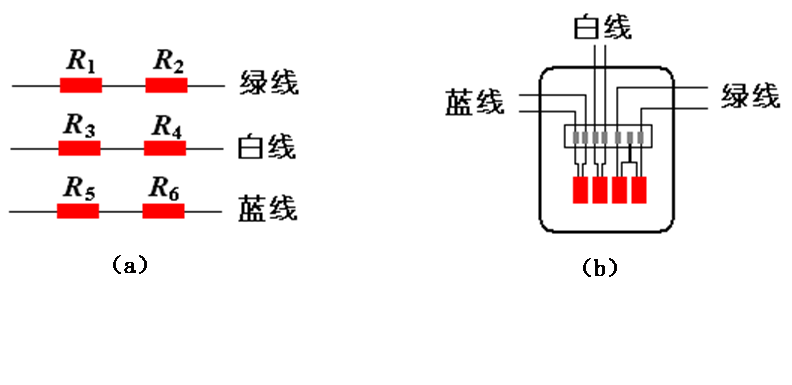
图5-4 应变片接线图
2. 实验步骤
1. 将试件按照轴对称施加荷载的方式加到装置上。
2. 打开测力仪开关,将应变片如图5-5串联单臂半桥接线法接至应变仪各通道上。
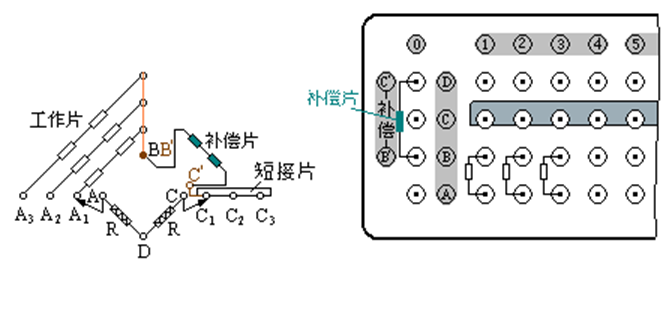
图5-5 串联单臂半桥接线法图
3. 检查应变仪灵敏系数与应变片是否相同,不同则设置成相同。
4. 进行实验:
a.加初始载荷0.3kN,将应变仪各通道置零。
b.加至1.3kN,记录读数。
c.退回至0.3kN,重新置零。
d.再加载至1.3kN,记录读数。如此步骤,重复三次。
5. 换到A-A位置加载,重复步骤4。
四、实验数据
表5-1 应变记录表
读数应变
载荷(F)KN |
R1与R2 |
R3与R4 |
R5与R6 |
|
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
|
通过对称轴线加载 |
ε1(με) |
ε2(με) |
ε3(με) |
|
0.3 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1.3 |
|
|
|
119 |
118 |
119 |
118.7 |
116 |
115 |
115 |
115.3 |
115 |
113 |
114 |
114 |
|
0.3 |
|
|
|
2 |
0 |
0 |
0.7 |
1 |
0 |
-1 |
0 |
2 |
0 |
1 |
1 |
|
沿A-A加载 |
εA1(με) |
εA2(με) |
εA3(με) |
|
0.3 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1.3 |
|
|
|
393 |
392 |
389 |
391.3 |
124 |
124 |
124 |
124 |
-148 |
-147 |
-147 |
-147.3 |
|
0.3 |
|
|
|
4 |
-1 |
0 |
1 |
0 |
-2 |
0 |
-0.7 |
-3 |
0 |
0 |
-1 |
五、数据处理
1. 根据实验数据计算出偏心拉伸时的拉应力、弯曲应力和横截面中性轴位置。
答:根据上面实验数据,结合材料力学相关知识计算如下:
(1)由实验数据可知,
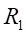
和
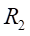
处的正应力值为:
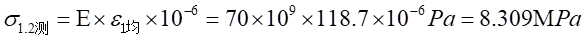
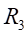
和
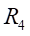
处的正应力值为:
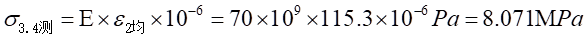
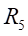
和
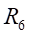
处的正应力值为:
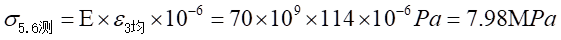
通过对称轴线加载时的平均应变为:
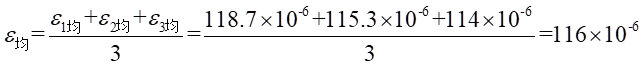
所以,拉应力为:
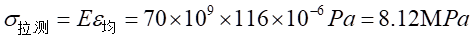
(2)由实验数据可知,通过
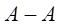
截面加载时
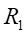
和
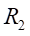
处的弯曲应力为:
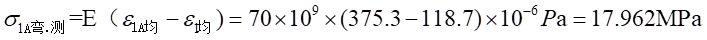
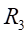
和
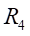
处的弯曲应力为:
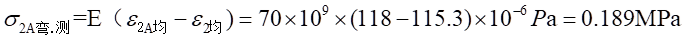
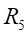
和
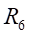
处的弯曲应力为:
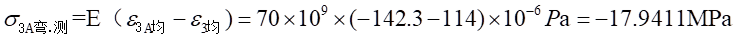
(3)距离中心轴距离为
y处总应力为:
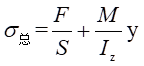
所以,设中性轴距离中心轴线距离为
y,则有:
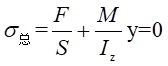
其中:
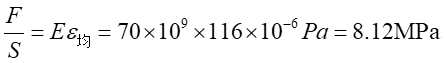
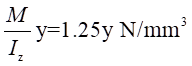
所以,可以得到:
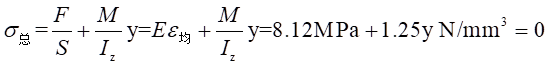
解得:
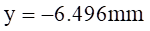
所以,横截面中性轴位置为:距离中心轴线
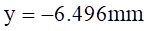
处。
2. 理论计算试件偏心拉伸时的拉应力、弯曲应力和横截面中性轴位置。
答:根据材料力学知识分析如下:
(1)拉应力为:
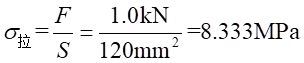
(2)弯曲应力为:
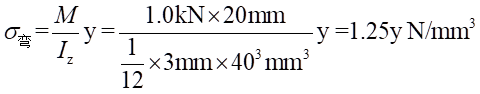
所以,距离中心轴线+15mm处的
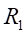
和
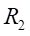
处的弯曲应力为:
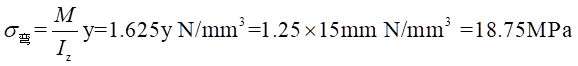
位于中心轴上的
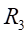
和
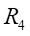
处的弯曲应力为:
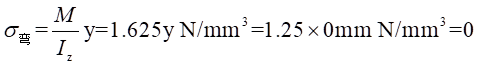
距离中心轴线-15mm处的
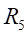
和
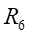
处的弯曲应力为:
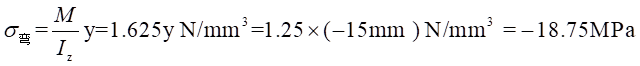
(3)距离中心轴距离为
y处总应力为:
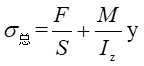
所以,设中性轴距离中心轴线距离为
y,则有:
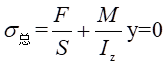
即:
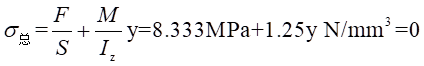
解得:
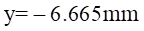
所以,横截面中性轴位置为:距离中心轴线
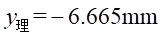
处。
4. 比较、分析实验结果与理论计算之差异。
答:结合材料力学相关知识计算如下:
(1)拉应力比较:
理论值:
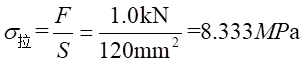
测量值:
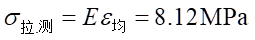
相对误差为:
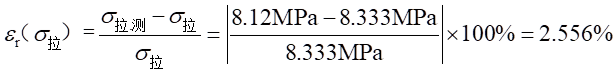
(2)弯曲应力比较:
a.应变片
R1和
R2处的弯曲应力:
理论值:

测量值:
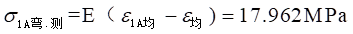
相对误差为:
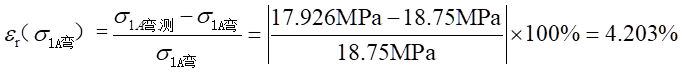
b.应变片
R3和
R4处的弯曲应力:
理论值:
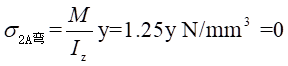
测量值:
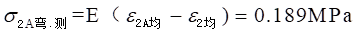
绝对误差为:
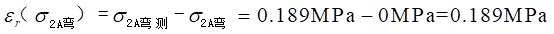
c.应变片
R5和
R6处的弯曲应力:
理论值:
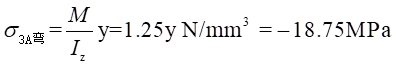
测量值:
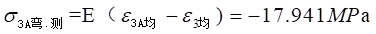
相对误差为:
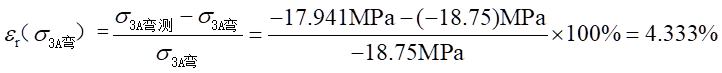
(3)横截面中性轴位置比较:
理论值:

测量值:
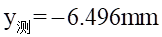
相对误差为:
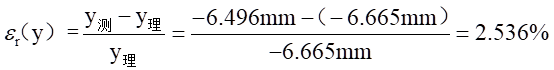
六、实验结果
根据前面计算可以看出,实验计算的结果和理论计算的结果基本吻合。现列表如下:
表5-2 结果对比表
|
比较对象 |
理论值 |
实验值 |
相对误差/% |
|
拉应力/MPa |
8.333 |
8.12 |
2.556 |
|
弯曲应力R1R2/MPa |
18.75 |
17.926 |
4.203 |
|
中性轴位置/mm |
-6.665 |
-6.496 |
2.536 |
从表中可以看出,理论计算和实验结果基本吻合,相对误差很小。实验从某种方面上证实了理论知识。数据可用性较高。
七、思考题
1. 本实验,若不采用通过试件对称轴和通过偏心A-A截面两次加载,是否能分离出分别由轴力引起的应力和由弯矩引起的应力?
答:能。该实验中轴力的作用效果是改变了中性轴位置。所以要想知道轴力的大小,我们实验研究的重点也应该是试件中性轴的变化情况。根据材料力学可以知道,所谓的中性轴也就是没有应变的轴线。所以所以我们可以通过实验找到中性轴的大小来反过来求轴力和弯矩引起的应力值的大小。
2. 本实验采用串联单臂半桥连接方式,可解决测试中出现的什么问题?
答:可以解决实验中出现的上下表面应变不同,从而提高实验的精度。
3. 当通过试件对称轴加载时,3组应变片(
R1和
R2,
R3和
R4,
R5和
R6)读数应变是否应该相同?
答:不相同。因为该实验这种加载施加的是集中载荷。材料力学公式的试用性是在圣维南原理的基础上。现实情况,截面上各个点的受力情况不尽相同,所以应变也不应该一样。但这并不能否认材料力学的知,我们用材料力学计算的结果已经很接近真实解,并且满足工程要求。