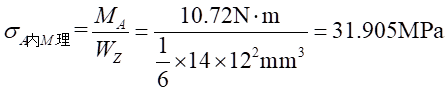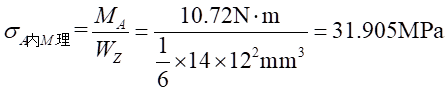圆框拉伸实验
一、实验目的
1.测定圆框试件(如图2所示)0至60º圆框内表面和外表面的切向应变分布,分析切向应变变化趋势,确定零应变位置。
2.测定圆框试件A
-A截面分别由轴力引起的应变和弯矩引起的应变。
3.与理论值进行比较、分析。
二、实验仪器和设备
1.拉压实验装置一台。
2.YJ-4501静态数字电阻应变仪一台。
3.圆框试件一个(已粘贴好应变片)。
三、实验原理及步骤
1. 实验原理
载荷
F作用在试件(见图8-1)的对称轴线上时,A-A截面有轴力,有弯矩,由于对称条件没有剪力。方框试件的弹性模量为70GN/m
2。轴力引起的正应力为:
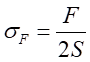
(8-1)
弯曲应力随着距离对称轴的距离大小不同而改变,但是其最大值是确定的,弯矩对A-A截面内圈处产生的弯曲正应力为:
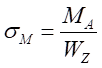
(8-2)
其中的
MA是A-A截面上的弯矩,
F是载荷。

图8-1 试件分析图
因此根据材料力学叠加原理,有
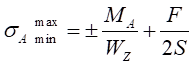
(8-3)
WZ为A-A截面的抗弯截面模量;
S为A-A截面的横截面面积。
2. 实验步骤
1. 将试件按照轴对称施加荷载的方式加到装置上。
2. 打开测力仪开关,将应变片以单臂半桥接线法接至应变仪各通道上。
3. 检查应变仪灵敏系数与应变片是否相同,不同则设置成相同。
4. 进行实验:
a.加初始载荷0.3kN,将应变仪各通道置零。
b.加至1.3kN,记录读数。
c.退回至0.3kN,重新置零。
d.再加载至1.3kN,记录读数。如此步骤,重复三次。
5. 将A-A截面应变片以双臂半桥接入电路,按照步骤4进行实验。
6. 将A-A截面应变片以对臂全桥接入电路,按照步骤4进行实验。
四、实验数据
表8-1 试件内表面应变表
读数应变
载荷
(F)KN |
A-A内表面
με |
白线4
με |
白线5
με |
|
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
|
0.3 |
|
|
|
|
|
|
|
0 |
3 |
0 |
1 |
0 |
2 |
0 |
0.7 |
|
1.3 |
|
|
|
|
|
|
|
315 |
311 |
313 |
313 |
206 |
204 |
204 |
204.7 |
读数应变
载荷
(F)KN |
白线6
με |
白线7
με |
白线8
με |
|
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
|
0.3 |
|
|
|
0 |
0 |
0 |
0 |
0 |
-2 |
1 |
-0.3 |
0 |
-4 |
1 |
-1 |
|
1.3 |
|
|
|
72 |
70 |
70 |
70.7 |
-102 |
-101 |
-101 |
-101.3 |
-293 |
-291 |
-292 |
-293.7 |
表8-2 试件外表面应变
读数应变
载荷
(F)KN |
A-A外表面
με |
绿线4
με |
绿线5
με |
|
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
|
0.3 |
|
|
|
|
|
|
|
0 |
-2 |
0 |
-0.7 |
0 |
0 |
0 |
0 |
|
1.3 |
|
|
|
|
|
|
|
-195 |
-193 |
-193 |
-193.7 |
-109 |
-108 |
-108 |
-109.3 |
读数应变
载荷
(F)KN |
绿线6
με |
绿线7
με |
绿线8
Με |
|
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
|
0.3 |
|
|
|
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0.7 |
0 |
3 |
-1 |
0.7 |
|
1.3 |
|
|
|
-6 |
-6 |
-6 |
-6 |
129 |
128 |
129 |
138.7 |
289 |
286 |
286 |
287 |
表8-3 A-A截面实验数据
读数应变
载荷
(F)KN |
A-A截面双臂半桥
με |
A-A截面对臂全桥
με |
|
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
1 |
2 |
3 |
平均 |
|
0.3 |
|
|
|
0 |
2 |
-1 |
0.3 |
0 |
0 |
-1 |
-0.3 |
|
1.3 |
|
|
|
683 |
678 |
679 |
680 |
146 |
145 |
147 |
146 |
|
|
|
|
|
|
|
|
|
|
|
|
|
五、数据处理
1. 根据实验数据,画出0至60度圆框内表面和外表面的环向应变分布,确定零应变位置。
答:
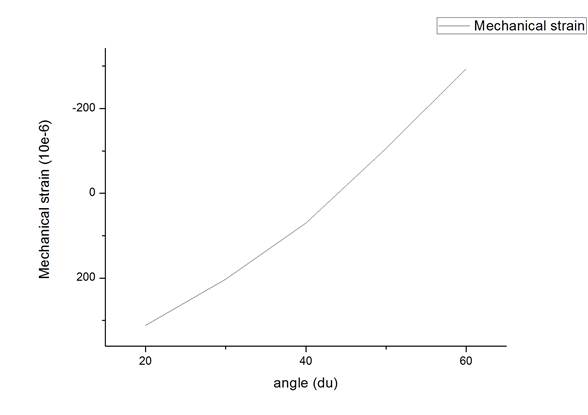
图8-2 圆框内表面的环向应变分布图

图8-3 圆框外表面的环向应变分布图
结合曲线走向,可以得出的结论为:
圆框内表面环向的零应变位置出现在

处。
圆框外表面环向的零应变位置出现在
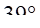
处。
2. 根据实验数据分别计算
A-A截面由轴力引起的应变和弯矩引起的正应力。
答:根据上面实验数据,结合材料力学相关知识计算如下:
(1)由实验数据可知,A-A截面由轴力引起的平均应变为:
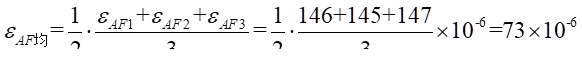
所以A-A截面由轴力引起的正应力为:
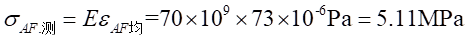
(2)由实验数据可知,A-A截面上内圈处由弯曲引起的平均应变为:
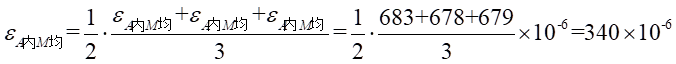
所以A-A截面上内圈处由弯曲引起的正应力为:
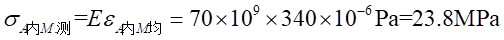
3. 根据实验数据分别计算A-A截面最大,最小正应力。
答:根据材料力学公式,截面总应力为:
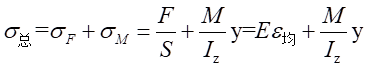
因此A-A截面的最大正应力为:
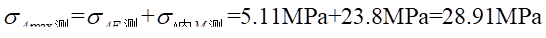
因此A-A截面的最小正应力为:

4. 理论计算A-A截面轴力、弯曲引起的正应力以及最大、最小应力。
答:根据材料力学知识分析如下:
(1)首先计算出A-A截面的弯矩。
由双对称条件,从A-A处截开,可知
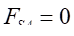
,

只有
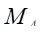
为多余约束,记为
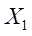
。因为截面A-A的转角为零,所以
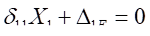
。
现计算
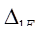
和
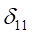
,方程如下:
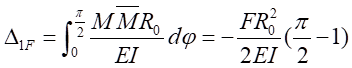
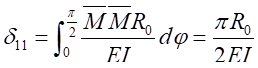
将
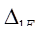
和
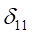
带入
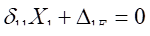
中去得:
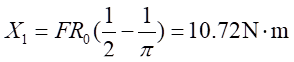
所以由轴力
F引起的正应力为:

A-A截面内圈处由弯矩引起的正应力为:
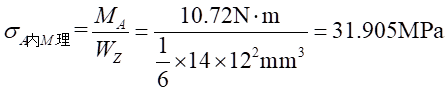
A-A截面的最大正应力为:
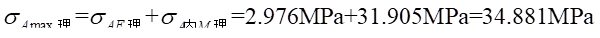
A-A截面的最小正应力为:
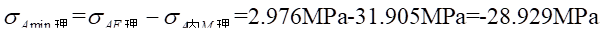
5. 比较、分析A-A截面实验结果与理论计算之差异。
答:结合材料力学相关知识计算如下:
(1)A-A截面由轴力引起的正应力比较:
理论值:

实验值:

相对误差:
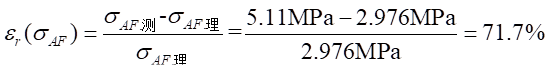
(2)A-A截面内圈由弯曲引起的正应力比较:
理论值:
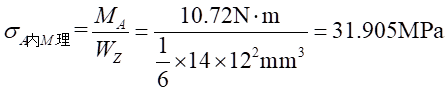
实验值:
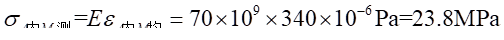
相对误差:
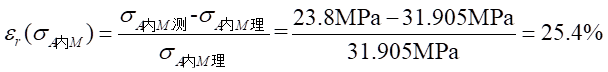
(3)A-A截面内最大正应力比较:
实验值:
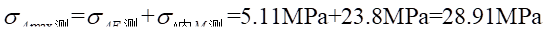
理论值:
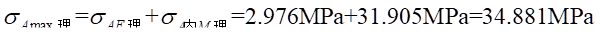
相对误差:
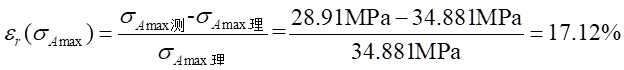
(4)A-A截面内最小正应力比较:
实验值:
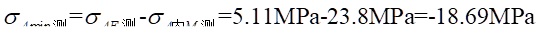
理论值:
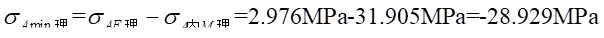
相对误差:
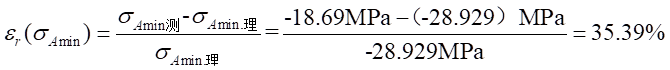
六、实验结果
根据前面计算可以看出,实验计算的结果和理论计算的结果基本吻合。现列表如下:
表8-4 结果比较表
|
比较对象 |
实验值 |
理论值 |
相对误差/% |
|
A-A截面拉应力/MPa |
5.11 |
2.98 |
71.7 |
|
A-A截面内圈弯曲正应力/MPa |
24.8 |
31.91 |
25.4 |
|
A-A截面最大正应力/MPa |
28.91 |
34.9 |
17.1 |
|
A-A截面最小正应力/MPa |
-18.69 |
-28.9 |
35.4 |
从表中可以看出,理论计算和实验结果除了第一个数据由于基数很小导致相对误差很大,但是考虑到绝对误差也是在可以接受的范围内的。其余数据基本吻合,相对误差较小。实验从某种方面上证实了理论知识。数据可以接受。
七、思考题
1. 本实验,是否可以同时测定圆框试件A-A截面分别由轴力引起的应变和弯矩引起的应变?提供组桥方案,并写出轴力和弯矩与读数应变的关系式。
答:可以。布片方案如下,在A-A截面内侧与纵向对称轴相交处贴应变片
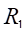
,外侧与纵向对称轴相交处贴应变片
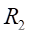
,并且在前后两侧竖向对称轴与
A-A截面交点贴上

和
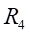
。
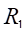
与
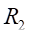
通过双臂半桥接线方法接入电路,得到的读数
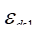
是弯曲引起的最大正应变的两倍;

与
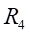
串联接入单臂半桥电路,得到的读数
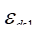
是轴力引起的正应变值。
轴力与读数应变的关系式为:
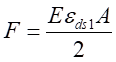
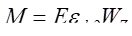
其中
A是试件的横截面面积,
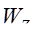
是试件横截面对中性轴的抗弯截面系数。
2. 简述本实验是如何分离出A-A截面上的拉伸正应力和弯曲正应力。
答:本实验可以通过双臂半桥组桥,得到的读数
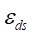
表示A-A截面上两倍的最大弯曲正应变,通过对臂全桥组桥,得到的读数
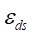
表示A-A截面上两倍的拉伸正应变。